数多あるデータ分析の手法の中で、重要な地位にある時系列分析。このブログではそんな時系列分析の考え方を解説したいと思います!
ブログ作成者紹介
Vareal株式会社
名前:Y.C
部署名:データサイエンス部
役職(ポジション):データサイエンティスト
業務内容:データエンジニアリング 大規模言語モデルを使用したプロダクト研究開発支援
趣味:ランニング ゲーム実況を見ること
時系列分析とは?
分析データの違い
データ分析や統計分析を書籍で勉強したことがある方なら、「回帰分析」というのはかなり序盤に目にするのではないかと思います。私が今まで色々な書籍をみてきた経験上、第3章くらいに「回帰分析」というカテゴリがあるイメージです。回帰分析について詳しく知りたい人は前回私が書いたブログで紹介していますのでぜひそちらをみていただきたいと思います。
「回帰分析」の後に「時系列分析」という章もあるかと思いきや、実はそうでないパターンがかなり多いです。普通の感覚ですと、回帰分析の際の分析対象データが時系列データになっただけなので大きく変わらないように思えるかもしれませんが、考え方が実は大きく異なります。
少し回帰分析のブログを振り返ってみましょう。前回のブログで提示したデータ例は、所得で消費を説明するというものでした。年収が500万円の人は年間消費額は◯万円というようなデータをもとに分析をしましたよね?これは時系列データではありません。データ自体はとある年度で統一したデータを持ってきて分析をしていることを仮定しているからです。年収500万円の人の年間消費額のデータは2023年のもので、年収800万円の人の年間消費額のデータは1996年のもので・・・と対象年度がバラバラでしたら良い分析にならないとは皆さんもイメージできると思います。
では時系列データとは何か?これも特に難しいことありません。例として、2000年の年収500万円の人の年間消費額のデータ、2001年の年収500万円の人の年間消費額のデータ・・・と同じ年収の人の年ごとのデータを持ってくればこれは時系列データとなります。「あれ?そうなると、年収800万円の人のデータはどうなるの?」と思う人もいるかと思いますがそこは分析目的の違いが出てきます。回帰分析では所得で消費を説明するという目的でしたが、時系列分析は過去の値で未来を予測することが目的になります。目的とデータの性質の違いが一度に出てきてこんがらがってしまったら申し訳ありませんが、分析の目的はまた後で説明するとして、時系列データとはどういうものかというのをまずここではイメージをしていただければと思います。
時系列データ
ざっくりとそれっぽく時系列データの説明をさせていただきましたが、基本的に皆さんがイメージされているような時間軸を考慮したデータが時系列データという認識で問題はありません。となると、結局のところ回帰分析の時と対して考え方は変わらないように思えるかもしれませんが、繰り返しですがそこに大きな違いがあります。今回のブログではその部分を簡単に紹介したいと思います!
ちなみに、弊社ではデータエンジニアリングからダッシュボード化やデータ分析の実施などデータに関してトータルでのご支援が可能です、興味を持っていただけましたらぜひお問合せください!⇨お問合せページ
時系列分析の考え方
データの捉え方
では、時系列分析についてもう少し詳しくみていきましょう。時系列分析を行う際に分析対象のデータは確率変数の集合と考えます。確率変数の考え方に関しましては、これも前回のデータ分析の手法のブログで説明させていただいたので、詳しくはそちらをみていただきたいと思いますが、確率変数の意味は、「様々な値を取る可能性があり、その可能性が確率で与えられている変数」と押さえておいていただければ大丈夫です。6面の通常サイコロの出目を確率変数Xとした時に、そのXのとりうる値は1〜6であり、その可能性は1/6という確率で与えられていますよね?これが確率変数の具体例となります。ちなみに、数学的にもう少し言うと、この確率変数は離散型の一様分布に従うと表現することができます。
分析データが確率変数の集合と考えると言うのはどういうことか?例えば経済変数の日経平均株価のデータを30年分集めてきたとします。このデータが確率変数の集合ということになるのですが、それは日経平均株価の値はさまざまな値を取る可能性があったが、観測値として今回はたまたまその値が得られたという考え方になるということです。例えば2024年7/25日の日経平均株価の終値が20000円としたら、色々な値を取る可能性があったが、7/25はたまたま20000円という値が観測されたという考え方が時系列分析の際のデータに対しての向き合い方なんですね。
確率過程
このような確率変数の集まりは、数学的に表現すると、次のように添字に時間であるtを取り表現します。
{…,Xt−2,Xt−1,Xt,Xt+1,Xt+2,…}
これを確率過程と言います。添字に時間を取って表現するというのは数学の中でもかなり稀な概念かと思われます。ですので言い換えると、時系列分析では分析データを確率過程として捉えると言うことになります。ちなみに確率過程の細かい定義は自分でも説明しきれず、確率過程というタイトルで1冊の本もあります。ここでは、添字に時間を取った確率変数の集まりと考えておきましょう。
こういった考え方の違いがあるので、回帰分析と時系列分析は考え方が異なってくるわけですね。そのため、繰り返しですが統計学とか計量分析などの書籍をみても、時系列分析の章がなかったりすることが多いです。確率の考え方も出てくるため割と基礎というよりは応用的なところもあり、時系列分析を勉強したい場合は時系列分析のような独立した書籍をあたらないといけないことが多いです。
こうして時系列分析のデータの捉え方がわかりましたので、次からは実際に時系列分析の方法やモデルなどをみていきましょう!余談ですが時系列モデルというのは、異時点間(時点tと時点t-s)の規則性を描写したものを言います。そしてその規則性を導き出すために色々考えたりすることを時系列分析と言ったりします。合わせてそのニュアンスも押さえておきましょう!
時系列モデル
定常性
さて、時系列データの考え方もわかったわけだし、早速分析していこう!といきたいところですが、分析をする際は確率過程にとある性質を想定しないといけません。それが定常性と言われるものです。ここからはかなり理論的に難しくなってくるのですがざっくりと説明をしていきたいと思います。以下の条件を満たす場合、その確率過程は定常の条件(弱定常性)を満たすと言います。
E[Xt]=μ
Var[Xt]=σ^2
Cov[Xt,Xt+h]=γ(h)
なんのことやらと思うかもしれませんが、右辺がtに依存していないというのがポイントです。細かい説明は省きますが、この概念は時系列分析、特に経済時系列分析では重要なものになりますので、さっと紹介をさせていただきました。
自己回帰(AR)モデル
さて、それでは最もシンプルな時系列モデルをみていきましょう!
それは、t期の値に関してt-1期という1期前の自分の値で定式化をするという以下のモデルです。
Xt=α+φXt-1+ μt
ちなみに回帰分析のシンプルな式は以下のようでした。
Yi=α+βXi+ μ
色々とデータの考え方は違いますが、モデルはかなり似ていますね。
モデルは似ていますが分析の動機は違うというのを気をつけておきましょう。回帰モデルでは、とある変数をとある説明変数で説明できないか?というのが目的になり、説明ができればその変数は重要な関係があるということがわかります。一方、時系列モデルでは来期を予想するのに、前期の自分の値を使って考えてみようというものです。経済学の領域では来期を予想するというのはとても重要です。それを実現するための最もシンプルな手法の1つがこの自己回帰モデルというわけですね。
例として想定したのは1期前のみですが、もちろん1期前と2期前で表現したモデルも想定することは可能で、例えば次のように一般化できます。
Xt=α+φ1Xt-1+φ2Xt-2+φ3Xt-3+…+φ?Xt-?+ μt
ただ、そうすると何期前までのモデルを作れば良いかという話にもなりますよね?例えば100期間分のデータが取れたとして、1〜25期間前までのモデルにするとかもできなくはないです。それを決める方法として(偏)自己相関という話もあるのですが、それはまた別の機会にしたいと思います。
本来は自己相関係数などから適切な次元数のモデルを想定するのですが、今回はその説明は省いて、この変数は1次元の自己回帰モデルで説明できるものと仮定して進めていきたいと思います。違和感がある方もいるかもしれませんが一旦そこは飲み込んで頂ければと思います。
こういった都合のよい、データXがあるとします。
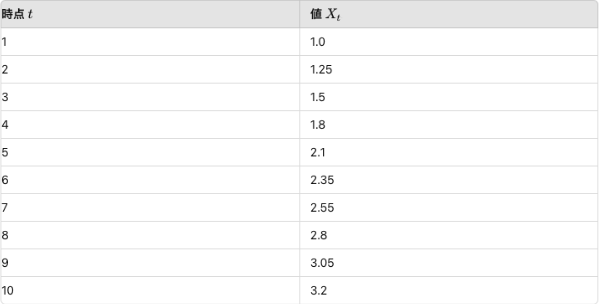
色々と分析した結果、このデータは1次元のARモデル(AR(1)と書きます)が適切ということがわかりました。あとは回帰分析と同じくパラメータの推定をしましょう!最小二乗法でこの数値からパラメータを推定したところ以下のようになりました。
Xt=0.45+0.72Xt-1
ということで、来期の数値は1期前の数値に0.72をかけて、0.45を足した数値で予測できるということがわかりました。
さらに、このモデルから生成される確率過程は先ほどさらっと出てきた定常の条件を満たします。なぜ満たすかというと、時系列モデルの定常の条件というのが、「パラメータについての特性方程式の根が単位円外に存在する」というものです。単位円というのは半径が1の円のことで、根は平方根の根です。これ以上の説明は省略しますがこの条件を満たしています。定常の条件を満たしているので良い分析結果と考えてよいです。逆に満たさない場合、モデルが良いものではなく、よい分析でなかったり、誤った結果を導いている可能性があるということになります。ということで、これで来期の値を算出してみましょう。
来期の値は0.45+0.72*3.2で計算でき、2.754と算出することができました。めでたしめでたし。
時系列分析の応用
グレンジャー因果性検定
時系列分析という切り口で因果関係を考えるというものも実はあります。それがグレンジャー因果性検定というものです。個人的にはかなり面白い理論だと思っていまして、詳細はまたどこかのブログで紹介できればと思いますが、簡単に説明をすると、とある変数を単変量時系列モデルで説明するのと、もう一つとある変数を入れた多変量時系列モデルで説明した場合、もし後者の方は説明力が上がったならば、追加でいれた変数から元々あるとある説明変数の方向に対してグレンジャーの意味で因果関係が成立すると定義したものです。ちなみに考案者のクライヴ・グレンジャーはノーベル経済学賞を受賞している有名な方で、時系列データ分析のスペシャリストの一人です。
未来の予測
今回の例はおそらく時系列分析の中で最も簡単なものかと思います。お恥ずかしいながら私が修士課程で勉強したくらいではそのほんの一部分しか理解できていませんし、応用理論は数学的にもかなり難解です。しかしやはり未来を予測するというのはやはりロマンがありますよね。時系列データの予測技術というのは、現代社会において非常に価値のあるツールとも言えるかと思います。企業はこれを使って売上を予測し、在庫管理や生産計画を最適化できますし、医療分野では、患者の健康データを分析して、病気の早期発見や予防策の提案に役立てることもできます。更には、気象予測により自然災害のリスクを低減し、私たちの安全を守ることも可能です。データサイエンティストとしてそういった使命感をもって(そしていつか競馬の予想が完璧にできる日を夢みて)今後も勉強に励んでいきたいと思います。

最後に
VarealではシステムコンサルティングをはじめとしてUI/UXデザイン・ソフトウェア開発・AI開発/データ基盤構築、開発後の運用保守まで、システム開発プロジェクトの要件定義フェーズ以降における全てのフェーズまでワンストップでご支援することも可能です。
なにかお役立ちできることがございましたら下記リンクよりお問い合わせくださいませ。










