データ分析と一言で言っても色々な考え方や手法があります、このブログではその中で最も基本的な概念である回帰分析について紹介したいと思います。
ブログ作成者紹介
Vareal株式会社
千田 康弘
部署名:データサイエンス部
役職(ポジション):データサイエンティスト
業務内容:データエンジニアリング 大規模言語モデルを使用したプロダクト研究開発支援
趣味:ランニング ゲーム実況を見ること
データ分析とは?
21世紀で最もセクシーな職業?
データサイエンス、ビッグデータ、データエンジニアリング、データアナリスト、データマイニングなどなどデータ分析やその役割に関するそれっぽい用語がここ15年位で色々と話題になってきました。その延長線上、あるいは最終到達地点に機械学習やAIもあると言ってもいいのかもしれません。上記のワードに関しては正直なところ自分の勉強不足なところはありますが、その定義はまちまちな印象もあります。一旦のところ細かい定義の確認は各自ChatGPTに聞いて頂くとして、いずれの用語もデータを分析する事柄に関わる概念であることは確かですね。
今から約12年前に、『Harvard Business Review』という、ハーバード・ビジネス・スクールが発行する経営雑誌の中で「データサイエンティストが21世紀で最もセクシーな職業である」と述べら、データサイエンティストというワードが話題となりました。この時期は歴史的に見てもデータ分析界隈が非常に湧いていた印象がありまして、日本では「統計学が最強の学問である」が出版された時期でもありますし、現在のAI発展のきっかけとなった画像認識の競技会ILSVRC(ImageNet Large Scale Visual Recognition Challenge)にてAlexNetが登場した時期でもあり、筆者が大学院に進学してデータ分析に関する研究者を目指した時期でもあります。
みんなも無意識にしているデータ分析
このように色々なワードやトピックがあったことからも、ここ10数年はデータ分析に関してとても注目されていた事がわかるかと思いますが、皆様はデータ分析というとどんな手段や手法をイメージするでしょうか?よく考えてみると、日常生活でも私たちは意識的に、あるいは無意識にデータ分析をしていたりもしますよね?例えば通勤や通学に関して最適なルートを検討したり、経験から混み具合を予測して空いている時間や場所を選択したり、料理を作る時も一部を抽出して分析(味見)をしたり、この人はこういう人だ、こういうことが得意だ、こういうことが苦手だなどなど人間の分析なども特に意識することなくしているのではないかと思います。
さて、日常生活のデータ分析はイメージしやすいかと思いますが、ビジネスの場ではどうでしょうか?これも皆様がデータサイエンティストではなくてもある程度イメージはできるかと思います。例えば、データをまとめたりエクセルやその他のツールで可視化することで現状や傾向を把握することは色々な部署で行なったりするかと思います。これは記述統計などと呼ばれたりします。さらに一歩進むと、そのデータに対してとあるモデルや手法を使用して法則を見つけ出したり予測をしたりすることも可能になります。前者の記述統計に関してはまたどこかでお話しさせて頂くとしまして、今回は後者にスポットを当てて、さらにその中でも最も基本的な考え方である、回帰分析についてお話をしていきたいと思います。
弊社では、AIや大規模言語モデルに関するソリューションはもちろん、データ分析やデータ分析をするためのデータ基盤構築からそれを効率的に運用するデータエンジニアリングまで、さらにさらに!開発と連携して既存のシステムに組み込んだり、新たにシステム開発を行なったりと、トータルで支援することが可能です!興味を持っていただけましたらぜひ、お気軽にお問合せくださいませ!⇨お問合せページ
単回帰モデル
回帰分析って何?
それでは分析の具体的な手法について詳しくみていきましょう。手法と一言で言っても色々な理論やモデルが存在していますが、その中でもよく聞くのは回帰分析ではないでしょうか?これはとある説明変数でとある変数(被説明変数と呼ばれます)を説明する手法で、統計学の教科書や私の専門分野の一つの計量経済分析の本でも、回帰分析は第3章くらいに出てくるまさにデータ分析の基本となる考え方です。モデルが線形であれば線形回帰モデル、非線形で例えばロジット関数を使うのであればロジスティック回帰モデル、説明変数が一つであれば単回帰モデル、説明変数が複数であれば重回帰モデル、など色々とモデルは存在していますが、ここではそのスタート地点でもある単回帰分析を説明していきたいと思います。
単回帰分析とは、先ほどさらっと説明した通り、とある説明変数1つで、とある変数(被説明変数)を説明する手法になります。ちなみに、先ほどからモデルと言ったり分析と言ったりしていますが、とある変数ととある変数の法則を考えることや導き出すことを分析と言いまして、その法則を数学的に書き表した式をモデルと言ったりします。それほど細かく考えずに同じような意味で捉えておいて問題はありません。今回は説明変数が1つですが、2つ以上の場合は重回帰分析と言います。変数が1つ増えるだけのように思えますが、それだけで色々と分析において考慮しておかないといけない概念も出てきます。今回はそこは考慮しなくて大丈夫なわけですね。
例を考えてみましょう。イメージしやすいものとして所得と消費の分析をしてみましょう!所得で消費を説明できるか?これを考えるということですね。なんとなく考えてみると、所得が多くなればその分消費も大きくなるんじゃないかと想像はできそうな気はします。
さて分析のためにはデータが必要ですが今回は次のようなデータを用意してみました。約20人の年間の所得とその人の年間の消費額ですね。ちなみにこれは総務省のデータとかそういったものはなく、それらしい値にしたダミーデータです。今回は単回帰分析の紹介のためなので、都合のいいデータを用意しました。
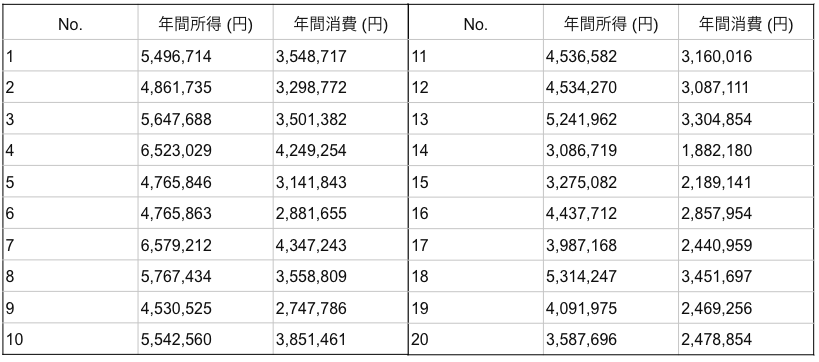
さて、これをプロットしてみましょう!横軸に所得、縦軸に消費をとって作図したのがこちらです!
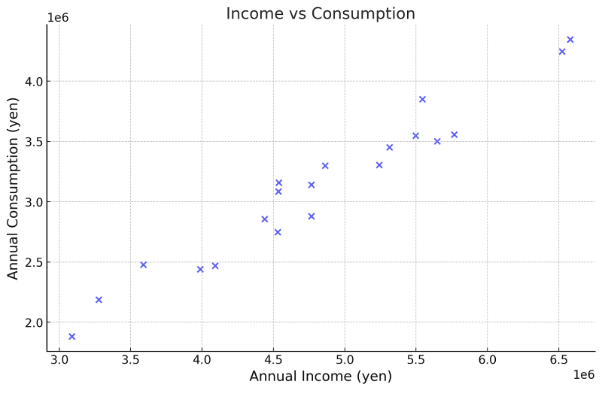
都合よく作ったデータなのでそりゃあそうなのですが、消費と所得にはなんらかの法則や関係がありそうですね。ではここで単回帰分析を試みようという話になるわけです。
単回帰モデルの式
では、より具体的に分析に進んで行きましょう。単回帰モデルというのは次のように表します。
y = a + bX + u
ここで簡単に各パラメータについて説明したいと思います。yは消費、Xは所得になります。aは定数項で、bは所得の係数です。このような法則が成り立つかどうかを考えるのが分析ということでありまして、成り立てば統計的に消費を所得で説明できるということになります。さらっと出てきましたが、uもとても大事な概念です。これは誤差項といいます。詳しい説明は字数的にできないためざっくりとした解説をしたいと思います。この誤差項ですが、これはとある特徴を持つ確率変数であると仮定します。確率変数とは何かという話もありますが、そもそもそれを厳密に知るためには確率論を理解していないといけません。
確率というのは、全ての事象を含む要素の集まりの集合と、その集合のそれ自身の集合を含む部分集合でありかつ特別な性質を満たす部分集合である加法族と定義し、その部分集合に確率を与える測度関数の三つからなる空間で定義されています。私は大学院では指導教官に「確率の定義は?」と聞かれた際に答えられないと怒られるため、上記のような内容をただ丸暗記して呪文のように唱えておりました。なので内容は全く分かっていないです。この概念の理解の先に確率変数の概念がありますが、確率変数とは確率空間におけるとある条件をみたす写像らしいです、一体なんなのかさっぱり意味がわかりませんね。ということで確率変数とは「色んな値を取る可能性をもつ変数で、その可能性が確率的に決まる変数」としておきましょう。誤差項をちょっと説明しようとするだけでこんな感じになってしまいますので、誤差項は良い感じの条件を満たす確率変数ということだけ抑えておきましょう。
モデルの推定
パラメータを推定しよう
こうして、分析するデータとそのデータを分析するためのモデルが定義できました。この後何をするかと言いますと・・・
y = a + bX + u
このモデルのパラメータであるaと、bを求めたいわけですね。そうすればモデルが完成するわけなので。じゃあデータを使ってどう求めれば良いの??ということですが、これをすることを推定と言います。推定の手法も色々と存在しているのですが、その中でも最も有名なのが最小二乗法と最尤法です。ちょっとこのタイミングで1つお話をしておきたいのですが、機械学習を勉強すると線形回帰というのが出てきます。そこでは予測をするためにモデルを学習するのですが、その際は勾配降下法というのが使われます。ここであまりごっちゃにしないでほしいのですが、今自分が行なっている単回帰分析と機械学習の線形回帰はモデルは同じなのですが目的が違います。なので、機械学習を勉強している人は一旦のところ、機械学習の線形回帰とは別で考えておいて頂ければと思います。
若干話題が逸れたというか、余計なことを言わない方が良かったような気もしますが、推定に話を戻しましょう。推定をする際に今回は最小二乗法を使用したいと思います。最小二乗法とは、誤差の二乗の和を最小にするようにパラメータを推定するというものです。なんとなくイメージを持てるのではないかと思いますが、ざっくりいうと、連立方程式を解いてaとbを求めるというそんな感じです。この最小二乗法で求められたパラメータは不偏性と有効性と一致性を満たすことで知られています。どういうことかと言いますと良い推定方法だということです!もちろんとある条件が満たせないとこの推定方法が使えませんので、そういう時は最尤法が使われたりしますが、今回は最小二乗法が使えるケースなのでこちらを使用するということでした。ちなみにこの手法は天体の軌道を予測するのに使われたらしいですね。
さてこうしてモデルを推定した結果、このようになりました!
y = -51,887 - 0.657X + u
はあ〜終わったぁ、じゃあ解散!としようとしたいところですが、後一個やることが残っております。それはこのモデルの妥当性の検証です。これには統計学の仮説検定というのを使用します。
モデルの検定
t検定をしよう!
モデルが無事にできあがったようですが、最後にこのモデル自体の検証をしなくてはいけません。「あれ?さっき最小二乗法を使えば色々な性質を満すって自慢してたんだから良いってことじゃないの?」と思う人もいるかもしれませんが、あれはあくまでパラメータの推定値が妥当かどうかということでありまして、そもそもこのモデル、つまり消費を所得で説明しようとすること自体が妥当かどうかということを統計的に検証する必要があります。モデルできたからそれでいいでしょ!とはならないわけですね。
そこで使用されるのがt検定というものです。これもまたまた説明すると仮説検定から話さないといけないのですが、都合の良いことに、前回私が以下のブログで説明をしておりますので、仮説検定についてはそちらを参照して頂ければと思います。⇨ブログ:統計的思考 〜統計分析と仮説検定〜
なので仮説検定をある程度把握しているというのを前提でお話をすると、ここでは、推定したパラメータのbが0という仮説を検定することになります(aは今回は置いておきましょう)。パラメータが0ということはどういうことだかお分かりになりますでしょうか?これは消費を所得で説明することができないということです。なので、t検定で仮説を棄却できないと、このモデル自体が成り立たないということになってしまうのですね。モデルをもう一度みておきますが、
y = -51,887 - 0.657X + u
bが今回は「0.657」でしたよね?これはかなり小さい数値で0に近いですよね?「あれ?そうするとこのモデル成立しないのでは・・?」という不安になる方もいるかもしれませんが、本当に「0.657」が小さいと言えるかどうかわかりませんよね?なのでt検定を使って統計的な結論を得るわけです。詳細は省きますが、今回t検定を実施したところ、bが0という仮説は強く棄却されました。なので、このモデルは妥当と言えるという結論を得ることができました。めでたしめでたし。
まとめ
こうして、とあるデータに対してモデルを使って推定して検定し、統計的に有意な結論を得ることができました。より具体的に表現すると消費を所得で説明することができたわけですね。このようにして、データを分析して法則を得ることができ、例えばその人の所得である程度の消費を予測することも可能になったわけです。先ほどは消費と所得のプロットを書いたかと思いますが、それに推定した直線を引いたものが以下になります。
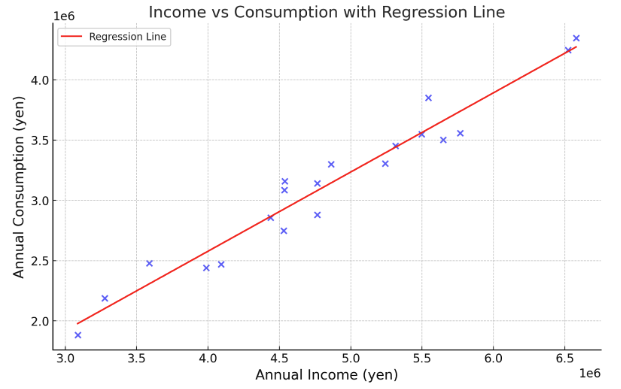
何度も申し上げているように都合のいい例なのできれいにできてる感はありますが、、例えば他の変数で応用することを考えるとするならば、広告費用と売上、教育年数と年収、気温とアイスの売上など分析をして回帰分析ができれば適切な予算や在庫、売上の予測などが可能になりそうですよね?こういった形で簡単に(精度の問題はありますが)データを使って分析ができるという例でございました。
ちなみに単回帰分析は数多ある分析手法の中で最も簡単なものです。まだまだ優れた分析手法やモデルは多く存在しています、データが有効活用できていない、活用の仕方がわからない、もっと色々な活用をしていきたいなど思っている企業の方がいらっしゃいましたら、ぜひお問合せくださいませ!こういった分析をして価値を提供していく仕事がしたいというデータサイエンティスト希望者の採用も行なっております!ぜひお気軽にご相談くださいませ!データと共にあれ。