ビッグデータやAIなど、ITの最新のトレンドの基礎には「統計学」の存在があります、このブログではそんな統計学の基本的な考え方について紹介をしてきたいと思います!
ブログ作成者紹介
Vareal株式会社
千田 康弘
部署名:データサイエンス部
役職(ポジション):データサイエンティスト
業務内容:データエンジニアリング 大規模言語モデルを使用したプロダクト研究開発支援
趣味:ランニング ピアノ
確率と統計
統計と確率はどう違うの?
突然ですが皆さんに問題です!あなたの前にいま扉が3つあります。そのうちの1つは当たり、残りの2つは不正解です。ここであなたはこれは当たりだ!と思った扉を1つ直感で選びました。するとこのタイミングで、司会の私が登場して、選んでない2のうち当たりではない扉をオープンしました。もちろん元々あなたが正解の扉を選んでいたら、両方ともハズレなので適当に選びますが、もし当たりの扉を選んでいなかったら、ハズレの方を選んでオープンしてあげるという事になります。
さて、ここであなたにもう一度選択のチャンスが訪れます。今の扉のままでもいいし、私がオープンしてない方の扉に変更してもいいという選択です。なんとも言えない選択権ですが、皆さんはどうしますか?ここで簡単に場合分けをすると、次のような4つに分られるかと思います。
①変更してもしなくても当たる確率は変わらない
⇨だって1個オープンしたから残り2個のうち一つで1/2じゃん!
②変更しない方が当たる確率が高い
⇨元々が1/3だったから変えたらもう一度試行を行うことになって1/3×1/2で1/6になる!そのままなら1/3のはず。
③変更した方が当たる確率が高い
⇨ハズレを開けてくれたことで、変更すれば2/3で当たることになる
④変更して当たる確率が変動するかは分からない
⇨そんなの関係ない、俺はどんな状況でも当たりを引ける人間だ
さて、この中のどれが正解でしょうか?これはとても有名な「モンティ・ホール問題」というものです。有名な数学者でも間違え、多くの議論を呼んだ問題です。
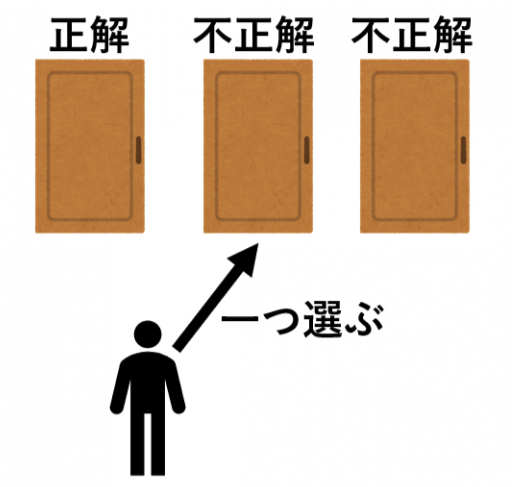
<画像引用元(学びTimes様):https://manabitimes.jp/math/989>
確率論あるいは確率的思考というのはこのように、ある事象の確率を仮定してそれに基づいて色々と物事を考えたり行動したりすることを言います。まさに「モンティ・ホール問題」も確率的思考の一つの例なのではないかと思います。
最も身近な例とすれば、天気予報などがそうではないでしょうか?午後の降水確率が90%であるならどうするか?多くの人が傘を持って家を出るかと思います。これもある種の確率的思考ですね。あるいはリスクというものを検討する際にも確率的思考というのはよく使われます。身近なものでもビジネスでも確率というものは使用されているということですね。
一方、統計学あるいは統計的思考というのはどういったことでしょうか?密接に関わってはいますが、実は少し考え方が違います。
このブログでは、統計分析についてや統計学独特の手法である仮説検定というものを紹介していきたいと思います!弊社ではデータ基盤の設計から、そのデータをもとにした分析やBIツールを使っての可視化など様々なご提案が可能です。
ご興味をお持ちいただけましたら、ぜひ、お問合せくださいませ!⇨お問合せページ
統計的思考
最強の学問?
2013年に出版された『統計学が最強の学問である(ダイヤモンド社)』という書籍を皆さんご存じでしたでしょうか?ちょうどその年は私が大学院に入りまさに計量経済分析で学者になるぞーと意気込んでいた時期でもありました。そんな中でまさに統計学が「最強」というタイトルはとても印象的で、自分だけでなく統計分析的な分野を専攻している人たちにとってはとてもワクワクするものだったかと思います。本の内容は各自見て頂くとして、統計的思考についてみていきたいと思います。

<画像引用元(ダイヤモンド社):https://www.diamond.co.jp/book/9784478022214.html>
話を引っ張りましたが、統計的思考はシンプルにデータから物事を考えること、あるいはそのプロセスを指します。さらに統計的思考の中には一般的には、記述統計と推測統計の二つの考え方があります。
記述統計はよく皆さんもビジネスで行なっているかと思います。グラフ化をすることで実在するデータの特徴や性質を把握する事、あるいはわかりやすく表現する事自体も記述統計と呼んだりすると考えてよいかと思います。「行為」と「方法」を記述統計としてしまってはいますが、ここではあまり細かいことは考えず、そういったことが記述統計なんだぁと思って頂ければと思います。
例えば
「このエリアは女性が多いぞ、よし女性向けの化粧品も置いてみよう」(行為)
「夜の交通量が少ないから、24時間営業しても意味ないな」(行為)
「学力をわかりやすく表現するために偏差値を使う」(方法)
これらはまさに記述統計、統計的思考ということになります。
母集団と標本
もう一つ、推測統計という統計的思考があります。これは考え方としては、標本から母集団を推定するというものです。母集団とは推測したい集団の全体のことで、標本は母集団の一部の集団というイメージです。
例えば、平均年収とか視聴率とかはまさに標本から母集団を推定している行為で統計的思考の推測統計というものです。よく、テレビでサラリーマンの平均年収というのを見かけると思いますが、アンケートを提出した記憶がある人はとても少ないかと思います。これは統計学的に言うと、一定の数を抽出してデータをとりその平均を求めるつまり標本平均で、母集団の平均を推定しているということになります。これはある程度の数を収集すれば、数学的に有効な数であることが証明される大数の法則というのが成立します。細かい説明は省きますが、統計的に言うと標本平均は多くの数を収集すればするほど真の値に近づくという「一致性」を満たすという事になります。
身近な例えをあげさせて頂きますと、皆さんお味噌汁を作る時に味見をしたりしますよね?その際に、おたまで軽くすくって小さいお皿に移してちょっと飲んで味を確かめたりすると思いますが、まさにそれは標本から母集団を推定しているに他なりません!まさか作ったお味噌汁を全部飲んで味を確かめる人はいないと思います。全てのサンプルを検査すればそれは確実ですが、それは現実的ではないですよね?特に料理の味見の時はそうです。母集団を推定するのに標本を使って推定を行う、これが統計的思考の推測統計といったものになります。

相関と因果
レコメンドシステムなどで利用される相関とは?
さて、統計的な考え方がある程度見えてきたところで、統計学で重要な概念の相関関係というのを見ていきたいと思います。非常に強力な分析手法の一つでございまして、色々と分析する上で非常に役立つ考え方です。
考え方はシンプルで名前の通り「相互に関係しあうもの」が相関です。例えば、消費と所得は相関関係にあるというのが、経済学でよく出てくるお話です。これは当然で所得が増えると、消費が増えるという関係性は容易に想像ができるかと思います。ここまではあくまでイメージの話ですが、相関関係の度合いを示すものとして、「相関係数」というものが数学的に定義されていまして、絶対値で0〜1の値を取り、絶対値で1に近いほど強い相関があり、0に近いほど相関がないという指標になります。

「相関係数」(2023年10月31日 (火) 12:00 UTCの版)『ウィキペディア日本語版』(https://ja.wikipedia.org/wiki/%E7%9B%B8%E9%96%A2%E4%BF%82%E6%95%B0)
この式の通り、相関係数は二変数間の関係を表すもので、分析をする上で大変有効な指標になります。ちなみに相関が強いということは、2次元での座標でより直線の関係にあるということを指します。よってAの値が増えた時にBの値も増える、あるいはAの値が減る時にBの値も減るような関係が強ければ強いほど直線になり相関が強いということになるわけですね。
因果関係とは?
しかし、ここで注意しておきたいのは、相関関係は因果関係とは別という点です。相関関係は単に相関係数が絶対値より1に近いかを言い表したもので、そこには原因と因果の関係がない可能性も十分に含まれていることも考えられます。ただ、因果関係がある可能性も十分に含まれているという点もあり、ここはなかなか難しいところです。
例えば、年収の高い人は高い財布を持っている、財布の価格が年収の200倍の法則というのがあるという話を聞いたことがあります。これは相関関係がありそうな印象はありますよね。高い年収の人はそれだけお金に余裕がありより良い財布を買うことができるからです。ただ、良い財布を持っていれば(原因)高い年収を得る(結果)ことができるかというとわからないところがありそうです、つまり財布の値段と年収には相関関係があっても因果関係はないという考え方ができます。なので、財布と年収なんか相関があるだけで因果関係はない、数字に騙されただけかぁという考えもありますが、それはわかりません!財布は常に肌身離さず持っているものです。その財布が良いものであれば、自分はこんな良い財布を持つのにふさわしい人間にならなくてはいけないという自覚が常に芽生え、より仕事に打ち込むことになり、結果的に良い財布であればあるほど良い仕事をするという事になり、結論として年収には因果関係が生じるという事は考えられるということになります。
若干脱線してしまいましたが、相関はとても強い道具ではありますが、因果をごっちゃにしてしまうのは危険な場合もあるという事でございました。ちなみに因果関係を数学的に考える因果推論という分野もありまして、個人的にもかなり興味深く大学院時代も少しかじっていました。コロナの感染者数増加や減少の原因の因果分析を行った事もありまして、なかなか面白い結果が出たのですがこれはまたの機会にお話をしたいと思います。
仮説検定
仮説を検定しよう!
さて、ここまでで統計的な考え方や手法というのを紹介してきました。これまでのお話は自分が説明をしなくても元々なんとなくイメージできていたり、日頃の生活やビジネスでも応用しているかと思います。ここからは、統計学の中で独特な手法である「仮説検定」というのを紹介していきたいと思います。統計学という本をめくるとだいたい第4章辺りに出てきて、かなりのページ数を割いている統計学の重要な概念の一つです。
ただ、始めに断っておきますと、印象として少し古典的な考え方ではあるかと思います。なぜかと申しますと、データが思うように取れないような時代で如何に統計的な判断を下すか?というための手法という点もあり、とてつもない量のデータにあふれている現代では手法としてあまり使われていない感じがしているからです。と言いますのも実は私の修士論文もこの仮説検定にまつわるものでございまして、「経済時系列分析をする際に、その確率過程が定常性の条件を満たすか検定を行う際に、帰無仮説のもとでの単位根過程が論理的に求められていない状況では有限標本おいてBeveridge-Nelson分解から絶対に判定ができないケースが生じてしまうという」という人生において全く必要のない論文を書いておりました。この経験上、体感として仮説検定にそのような感覚を持っております。
私の論文はさておき、仮説検定自体は使われてないような印象が少しあるとはいえ、面白い考え方で統計学を象徴するものでもあるのでここで紹介をしていきたいと思います!
今回は例として、インスタントの味噌汁の塩分濃度を考えてみましょう。その工場では、規定として塩分濃度7%で作っています。しかし最近、「塩分濃度高いのでは?」という声がお客様から寄せられました。そこで「じゃあ塩分のチェックをしよう!」となった時に、もちろん、工場を一回止めて何百何千とある全てのインスタント味噌汁をみんなで開けてお湯を入れてチェックすれば塩分濃度が増えたかどうか確実に分かりますが、それは非現実的ですよね?そこで、お待ちかねの仮説検定君の登場です。
ではここから仮説検定をおこなっていきたいと思いますが、細かい仮定や説明を省いている点はご了承ください。ここでは仮説検定でこういうことができるんだというイメージを持って頂ければと思います。
まず検定仮説(帰無仮説)と対立仮説を用意します。
・帰無仮説:塩分濃度は規定の7%のまま変わっていない お客さんの気のせい
・対立仮説:塩分濃度が規定の7%より高い 謝罪案件
ここでサンプルとして無作為に49個インスタント味噌汁を選んで、お湯を注いで塩分濃度計をいれて塩分を計測しデータを取るという実験を1度行います。
ここで
・母平均は7%
・母標準偏差は既知として1.1
・抽出したお味噌汁の数49
・49個のインスタント味噌汁の濃度を測って平均を取ったら7.4%
と仮定します。
直感的には7.4%なのでちょっとだけ濃度が高くなったと考えることもできますが、これは誤差の範囲の可能性もあります。それを統計的に判定するのが繰り返しですが仮説検定です。
次に検定統計量を用意することになります。が、これは確率変数です。ここら辺はかなり込み入った話になってきますので、ささっと通過したいとは思いますが、ここで使う標本平均の分布については、中心極限定理というそれで本が一冊あるくらいの統計学の世界で最も有名な定理がありまして、この定理により標本平均の確率分布が正規分布に従い、かつパラメータも求めることができます。この定理があるため検定統計量が正規分布に従うことになり、標準化をして標準正規分布として扱いが可能となり、任意で決めた有意水準の元で帰無仮説が棄却できるかどうかを判定することができます。
堅苦しい話は置いておいて、検定統計量を式に当てはめて作ってみます。
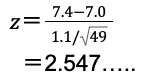
こうして検定統計量の値を求めることができました。ここで有意水準は5%としましょう。
今回は片側検定になっており、その時に棄却域の境界点は1.64となります。この値より2.54は大きいためこれは棄却域に入ったという事になりました。これはどういうことかといいますと、もし上記の条件で検定を行ったら、濃度が7.0%だった場合に、今回のような平均が7.4%という結果が出る確率はかなり低い、ということは7.0%という前提が間違っていますね!という論理展開になります。これが統計的な仮説検定ということです。
さて、こうしてめでたしめでたし、帰無仮説が棄却され、対立仮説が採択されます。つまり統計学的には、塩分濃度が規定の7%より多いという状況になりました。ですので、工場はすぐに設備の点検などをして、塩分が規定より高くなってしまった原因の調査をしなくてはいけないということになりますね。
はい、ということで、全く説明していない用語もいきなり出現してまして、よく意味がわからなかった方も多いかと思いますが、これが統計的仮説検定の考え方になります。ちょっと独特な考え方ではあり腑に落ちないところもあるかもしれませんが、数学的な証明とは違う統計的な思考方法というもののイメージが少しでもついて頂ければと思います。
思考方法の違い
こうして統計学がやりたい事がなんとなくお分かり頂けたかと思います。データを収集してそのデータをもとに真実に近づいていくことが統計学の一つの目的です。
一方で冒頭の「モンティ・ホール問題」は確率的な思考でした。この状況でどういう事がこれから起こるのか考えるのが確率論の一つの目的ということでございます。ちなみに「モンティ・ホール問題」の正解は3で、扉を変えると正解する確率は2/3となります。ググッと正解の可能性が上がるというなかなか直感的に理解しにくい結果でした。特に解答で「①変更してもしなくても当たる確率は変わらない」を選んでた人は違和感があるかもしれません。
それではこのように考えてみましょう!もし扉が全部で100個あり、当たりが1つとします。あなたが1個選んで、残りの99個残ってますね?司会の私がその99個の内、もしあなたがハズレを引いていたら、残りの99個のうちハズレの98個をオープンします。もしあなたが当たりを引いていたら、残りの99個どれもハズレなので適当に98個オープンするということになります。さてこの状況であれば、あなたは扉を変えようとするのではないでしょうか?考えようによっては、今あなたが選んでいる扉か、98個オープンされた後の扉の2個なので、当たる確率は1/2じゃないかという考え方もあるかもしれませんが、、、最初のケースよりは扉を変えた方が当たる確率が上がるという点は納得できるのではないでしょうか?確率を考える際は極端な例を考えると割とイメージしやすくなることがありますので皆さんもぜひ活用ください。
標本の大きさは?
はい、ということで、大変ありがたくも最後までお付き合い頂きました読者の方に統計の小話をひとつ、先ほどの仮説検定の味噌汁の例を思い出して頂きたいと思います。サンプルとして無作為に49個インスタント味噌汁を選んで、お湯を注いで塩分濃度形をいれて塩分を計測しデータを取るという実験を1度行いましたね。そしてその49個の平均塩分濃度が7.4%でした。さてこのとき、この検定の標本数(サンプル数)はいくつでしょうか?
・・・49と答えたいところかもしれませんが、これは誤りです。この問題はある種、統計学を勉強したかどうかを示す試金石となっているものです。
弊社では統計分析をするためのデータ基盤構築からデータの可視化や統計分析を使った提案型のコンサルティングなどトータルでご協力させて頂きます、興味を持って頂けた方、標本数の答えを知りたい方は是非ともお問合せくださいませ!⇨案件のお問合せ
一緒に働きたい方も募集中!X(Twitter)では社内の雰囲気を発信しています、ぜひフォローしてみてください!
採用ページ
弊社公式X(Twitter)
弊社オリジナルキャラクターバレアルマンX(Twitter)