データ分析の手法シリーズ!今回は主成分分析について紹介いたします!
ブログ作成者紹介
Vareal株式会社
名前:Y.C
部署名:データサイエンス部
役職(ポジション):データサイエンティスト
業務内容:LLMを使用したプロダクト開発 人事データDX支援
趣味:ランニング ボクササイズ ピアノ
いつもの
選べない男
私はたまにではありますが、勉強や研究に行き詰まった際にはカッコをつけてBarに行ったりすることがあります。正直お酒についてよく分かっていないですが、そのお店に初めて行った際に、とりあえずウィスキーのロックを頼みました。そのウィスキーはそれほど好きなわけではなく、カクテルなども頼んでみたいという気持ちはあるのですが、種類があり過ぎて何を選んで良いかわからないのと、ロックを飲むのが周りからみても渋くてかっこいいのかなというのもあり、最近は半分嫌々でまず『グレンリヴェット12年』を頼んでいます。
行きつけの町中華も、安くて美味しいメニューやお酒がたくさんあるのですが、ここでも選べぶことができずに、結局同じものを頼んでいたため、お店に入るといつものいらっしゃるおそらく中国人の女性の店員さんから「いらっしゃいませ」の前に、「レモンサワー?」と言われます。そのあと、その人がレモンサワーをテーブルに持ってくると「青菜炒め?」と言われて頷くみたいな展開になります。先日は、まだレモンサワーが2/3ほど残っているのにおかわりのレモンサワーを「持ってきちゃった♡」と言われてテーブルに置かれました。さすがにそれは早すぎな気はしますが、結局レモンサワーしか頼めない男ですから、スムーズに二杯目にも移行できたので良しとしましょう。
豊富なメニューがあることは魅力的である一方、私のような優柔不断な男には種類が多すぎると適切に選ぶことができずに結局同じものを選ぶことになったりしてしまうことがあります。まあどちらのお店でも結果満足して帰るから良いんですけどね。
データの選択
このような状況はデータ解析でもそうであったりします。データは多いに越したことはないという側面はある一方で、解釈が難しくなったり、モデルを作る際にデータ同士が相関を持ってしまうことで多重共線性という問題が生じたり、分析に使うべきでないデータも混在していて結果的にノイズとなってしまい分析精度が下がってしまったりと、、データのメニューでも豊富すぎて適切選べなかったり、多すぎる故に満足度が思ったほど上がらなかったりなんてことがあったりするわけですね。
まあ私のウィスキーのようにいつも同じものを選ぶ羽目になるということはデータ分析においてはないかと思いますが、こんな時にデータを性質を集約したり、より解釈しやすい方向に持っていくことができる手法が統計分析の中にいくつかあります。その中の「主成分分析」というものを今回のブログでは紹介していきたいと思います!
弊社ではデータ分析やデータ可視化のご支援も可能です、もし興味を持っていただけましたらぜひお問い合わせくださいませ!
データの情報量とは?
ラーメン屋さんでのケーススタディ
データを見てどれが重要な項目なのか、どう解釈すればいいのか・・・皆さんはどうやって判断しますでしょうか?例えば、分かりやすく(?)あなたは、ラーメン屋さんを経営しているとしましょう。ここで、テーブルの上にアンケートを置いておいて、【注文の待ち時間に記入してくれたら味玉無料プレゼントキャンペーン】を実施してお客さんの評価を収集し、その結果をもとにしてうちのラーメンを食べてくれるお客さんはどういったことに魅力を感じているか?その結果からどういう新商品やサービスを展開していくべきか?ということを分析して更なる売上の向上を図る施策をしていくというケースを考えてみましょう。
ラーメン屋さんが人気の理由は色々考えられますよね?安いとか、野菜が大盛りでこってりとか、ご飯無料とか、ご主人が面白いとか、周りにラーメン屋さんがないからとか、大きく入りやすい駐車場があるからとか、、そのお店ごとに色々な魅力があるはずなのにも拘らず、適切にその需要を見極めることができずに、例えば周りに学生が多く、大盛りやご飯無料に魅力があるのに新たに駐車場を拡大するとか、あっさりとしたスープが女性やファミリー層に対して魅力だったのに濃厚さを足してみてしまったりとかすると、逆効果になったりする可能性がありますよね?
という事で、ここでは改めてアンケートを取って、うちの強みや今後の方向性を的確に把握し経営戦略を練っていくことを考えていきましょう〜。
平均は同じでも
アンケート内容は皆さんが想定していそうな内容で問題ないかなと思います。例えば全てを10段階評価みたいな感じで置いておいて、味、濃厚度、あっさり度、値段、メニューの豊富さ、見た目、トッピング、ボリューム、立地、入りやすさ、居心地などなどそういったものをイメージしてくれれば大丈夫かと思います。
実際にアンケートを収集して、集計したとしましょう!10段階の数値の例えば平均をみたとして、
「味は7.5かぁ〜ふむふみ」
「おっ、意外にも居心地が感じてくれてるのか!」
「バズりを狙った商品を作ったけど、あまり見た目のウケが良くなかったか」
など色々と知ることができるかと思います。
こうして色々なお客さんの声を聞くことはできますが、それをどう解釈すればいいか?色々聞きすぎてどれを重視すればいいか?都合の良い結果や改善しやすそうな項目を見てしまってはいないか?私はどのカクテルを頼めば良いのか?レモンサワーだけじゃなくビールを頼むかもしんないじゃん。などなど、迷いが出てくる可能性もあります。
ここで、もう一歩進んだ分析をしていくことを考えてみます。言ってしまえばそれが今回の主成分分析です!という話にはなるのですが、まずはこの主成分分析の考え方を簡単に紹介していきたいと思います。
主成分分析のキーワードとして重要な概念がありまして、それが『分散』です。これは統計用語でございまして、数学的に定義は存在しています。数学的な定義をお見せして「はい、これが分散でした、本当にありがとうございました」というのはつまらないのでこの分散を説明していきたいと思います。
数学的な定義ではなくざっくりと分散の意味を説明したいのですが、そのためには期待値という概念を押さえておく必要があります。「ちょっと待ちなさいよ、じゃあその期待値を理解するには、また何か別の概念を知る必要があるんじゃないでしょうね?」と思われる奥様もいらっしゃるかもしれませんがそれはその通りです。ただ、そうすると際限がないので期待値までで踏みとどまりましょう。
期待値は誤解を恐れずに言えば「平均」です。平均も細かく言うと実は色んな平均があるのですが、いわゆる全部足してそのデータの数で割る算術平均です。これを一旦期待値と思って進めましょう。
さてさて、ではその期待値を押さえた上で、『分散』とはどういうものかと言いますと、「データの取りうる値と期待値との差の2乗の期待値」になります。・・・うーん、で、それは結局なんなの?となってしまうかもしれませんが、ざっくり言うと期待値がそのデータの代表的な数値を表している指標である一方で、分散はそのデータの散らばり具合を表している指標です。分散が大きいと、そのデータがとても散らばっている、一方で小さいと散らばっていないということになります。
先ほどのアンケートの例で言うと、味に関して1点をつける人もいれば、10点満点をつける人もいた場合、味というデータの分散は大きくなり、極端な話ですが、メニューの豊富さに関してアンケートを答えた人の回答が全てが5点だった場合、全く散らばっていないので分散は0になります。
このように分散の数値を見るだけでそのデータの散らばり具合がなんとなくイメージできるんですね。ただ、注意ですが本当になんとなくです。分散が100の場合どうか、10000の場合どうかみたいなのは分散単独でみても解釈は難しいかと思います。そのため、とあるデータとデータで分散を見比べることで解釈できることがあります。例えば味と値段の100人のアンケートの平均得点が5点だとしても、味の分散が10000で、値段の分散が0.01だったとします。そうすると、同じスコアであったとしてもなんか意味が違うように感じてきますよね?
分散にこそ価値がある
さて、こうして分散の意味と、平均得点だけみても、それだけでは理解できない部分があることがなんとなくイメージできたのではないでしょうか?ここで注目すべき点は、主成分分析の考え方として「分散が大きいデータは情報量が多い」と考えるところです。
先ほどのラーメン屋のアンケートの例で再度考えてみましょう。味の評価平均は10段階の真ん中の5点、値段も同じく真ん中の5点、ただ、味の分散は大きく評価が散らばっているのであれば、そこに改善の余地があるように思えますよね?逆に、ほぼ満場一致で値段の評価が5点であれば、「まあみんな値段に関しては可もなく不可もなくかぁ」という印象を持つのではないでしょうか?この場合、味と値段のデータの情報として重要なのは、味だと考えることができます。(注意ですが、これはあくまで分散や主成分分析という考え方においてということであって、例えばほぼ全員がアンケートで1の評価をしているものがあればそれを改善した方が当然良いということは明らかです、ただその考えは一旦置いておきましょう〜)
皆さんの感想がほぼ一緒の項目より、意見がばらつく項目の方がデータの情報量が多く影響度が高い、この考え方が主成分分析にあるというのをなんとなくイメージできれば幸いです。もちろん主成分分析以外でもこの考え方を持つことはデータを正しく解釈する上で重要ですので、覚えておいていただければと思います!
その項目はどれだけ寄与しているの?
分散行列と固有値分解
ここまででなんとなく主成分分析の狙いみたいなのがわかっていただけたのではないでしょうか?ここからは具体的に主成分分析のアプローチをみていきましょう!
ちなみにここでちょっと補足ですが、主成分分析はラーメン屋の例のようなデータをより深く分析するという趣旨もありますが、もう一つ次元削減という意味もあります。一旦ここはデータをより深く分析していくアプローチの意味での主成分分析として進めていきたいと思います。(実際は次元削減という意味合いで主成分分析が出てくる方が多いかもしれません)
主成分分析の手順を簡単に説明しますと次のようになります。
①どのご家庭にもあるデータの分散共分散行列を用意します。
②そしてその分散共分散行列に対してみんな大好き固有値固有ベクトル分解を行います。
③そして、その固有値が大きい順にその固有値に対応する固有ベクトルをいくつか取ってきます。それが主成分です。さあお熱いうちに召し上がり下さいませ。
なんかよくわからん用語が急に色々出てきましたがそこは安心していただいて大丈夫です。実際はこれを一個一個手で計算して行うということは今の時代あまりなく、pythonやR、それ以外のプログラミング言語でも主成分分析を行うライブラリがありますのでそれを使えばあっという間に計算はできます。細かくその手法を理解できていなくても主成分分析を行うことはできますので安心してください!
ただせっかくなので簡単に出てきた用語をみていきましょう!お恥ずかしい話自分も完全に理解できていない部分があります。もし間違っていたら申し訳ないというのと同時にご教授いただきたいと思っております。
固有値分解とは、とある行列に対して行う分解の手法になります。主成分分析ではもちろんその行列は分散共分散行列です。行列Aに対して、
A=QΛQt
となるような、
Q: 固有ベクトルを並べた行列
Λ: 対角成分が固有値の対角行列
を探し分解することが、固有値分解です。
じゃあそれを満たす固有値と固有ベクトルは具体的にどう求めるか?といいますと、上記は行列全体で一般化したもの(並べたとあるように)で個々の具体的な固有値と固有ベクトルに話を落とし込みますと、
AX=λX
A: 対象となる行列(PCAでは分散共分散行列 )
λ: 固有値(スカラー)
X: 固有ベクトル(行列の特性を反映した方向ベクトル)
と式として表すことができます。
ここでベクトルと行列の関係に関して簡単に説明しておきますと、簡単に表現すれば行列は数や文字の集まりで、ベクトルはその行列の特別なケースと考えることができます。今回その行列とやらが分散共分散行列なわけですが、その行列について、固有値と固有ベクトルというのを求めるということを行う=固有値分解を実施するということになります。この固有値はその行列における情報の多さを示し、固有ベクトルはその方向の情報をもちます。なので情報として重要な分散の集まりの行列に対して、固有値の高い順にその固有ベクトルを持ってきます。その際に固有値が最も高いものを第一主成分といい、二番目は第二主成分と続きます。そして、固有ベクトルと実際のデータを使ってとある計算をすること主成分スコアというものを得ることができます。これが主成分分析といわれるデータ解析の方法でございました。
こうすることで、情報を集約しより深くデータを理解することができます。
お客さんは何を求めているか
主成分分析やってみた
さて色々と、偉そうにごちゃごちゃ説明をしてきましたが、最後に簡単な例をお見せしていきたいと思います。
引き続き簡単なラーメンの例で見ていきたいと思います。あくまで例なのであまり厳密な数値ではないですが、そこはそのくらいで見ておいて頂ければと思います。
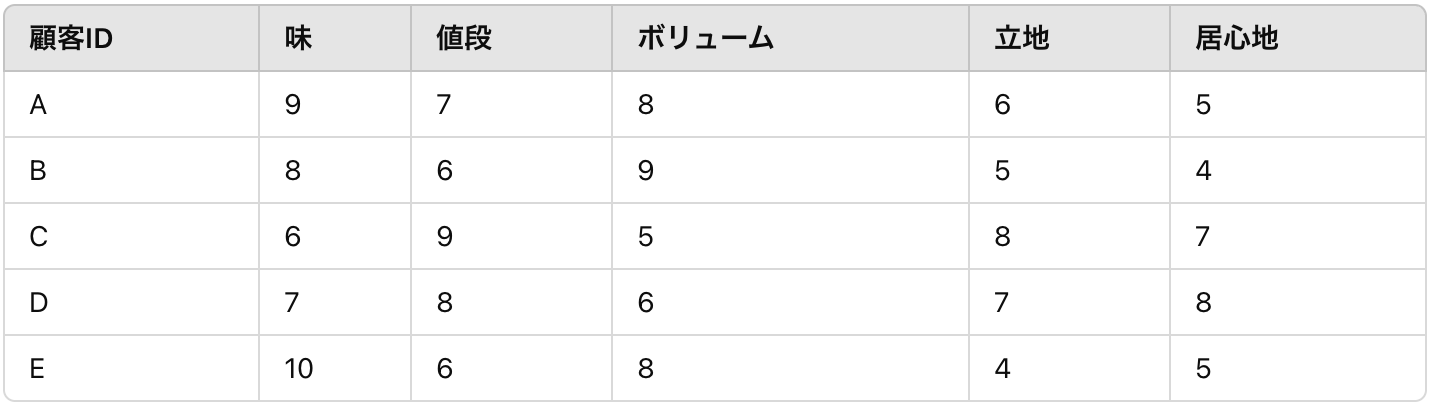
人のお客さんの例で、アンケート結果はわかりやすく一旦5個にしました。簡単にするために5個にしたせいで主成分分析をしなくても解釈できそうですが、そこは一旦置いておいてください。
そして、、このデータを主成分分析のライブラリに突っ込んでみます。すると次のような結果が得られました。

こんなに綺麗に3個に普通は収まらないですがあくまで例なのでご容赦頂ければと思います。固有値を見ての通り大きい順に並んでいますよね、そして、寄与率というのがありますが、これがその情報量の締める割合と考えて良いです。つまり、アンケート結果は、第1主成分で7割、第2主成分で2割、この二つの成分でアンケートの情報の9割を説明できるということになります!ということは、アンケートでは5個の項目でどれに注目すれば良いか迷ってしまうあなたでも、この1つの成分に注目すれば7割の影響度を把握できる、2つの成分なら9割の影響度を把握できるということになるのですね!
さて、それでは第1主成分と第2主成分の各固有ベクトルをみてみましょう。これは主成分分析の文脈では負荷量(主成分ごとに元の変数がどの程度寄与しているか)と言われたりします。
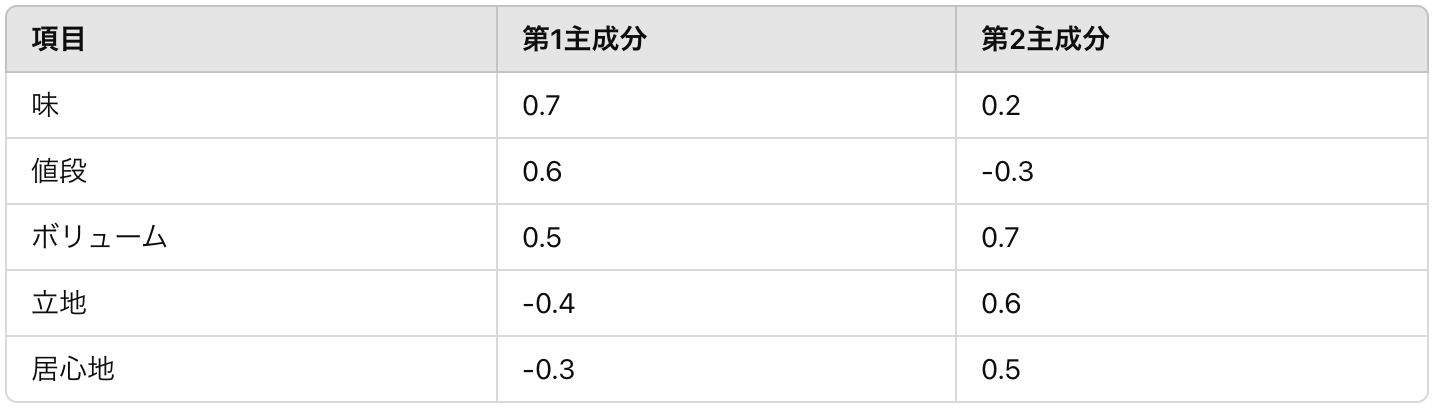
これを見ると、第1主成分は味、値段の要素を強く反映していて、第2主成分は、立地や居心地の要素を強く反映してそうです。ボリュームはどちらの主成分でも同じように影響を持っていて、もしかするととても重要な要素であるかもしれません。
最後にこれをスコア化します。
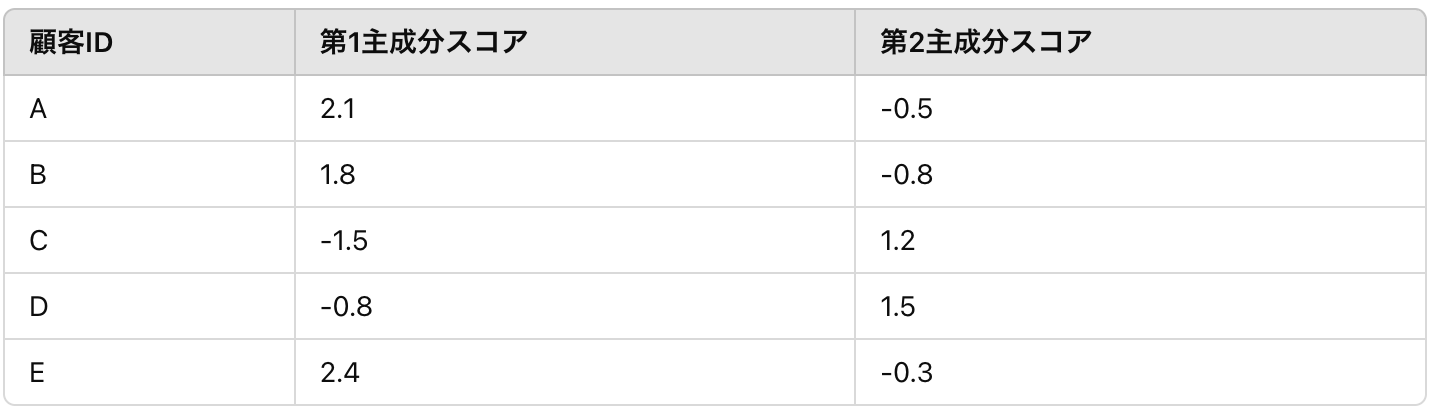
5個のアンケート結果が2つの要素に集約できました。分散というワードを使って言えば、分散の大きい方向に変数を射影して新たな変数を得たということになります。
このスコアをプロットするとこうなります。
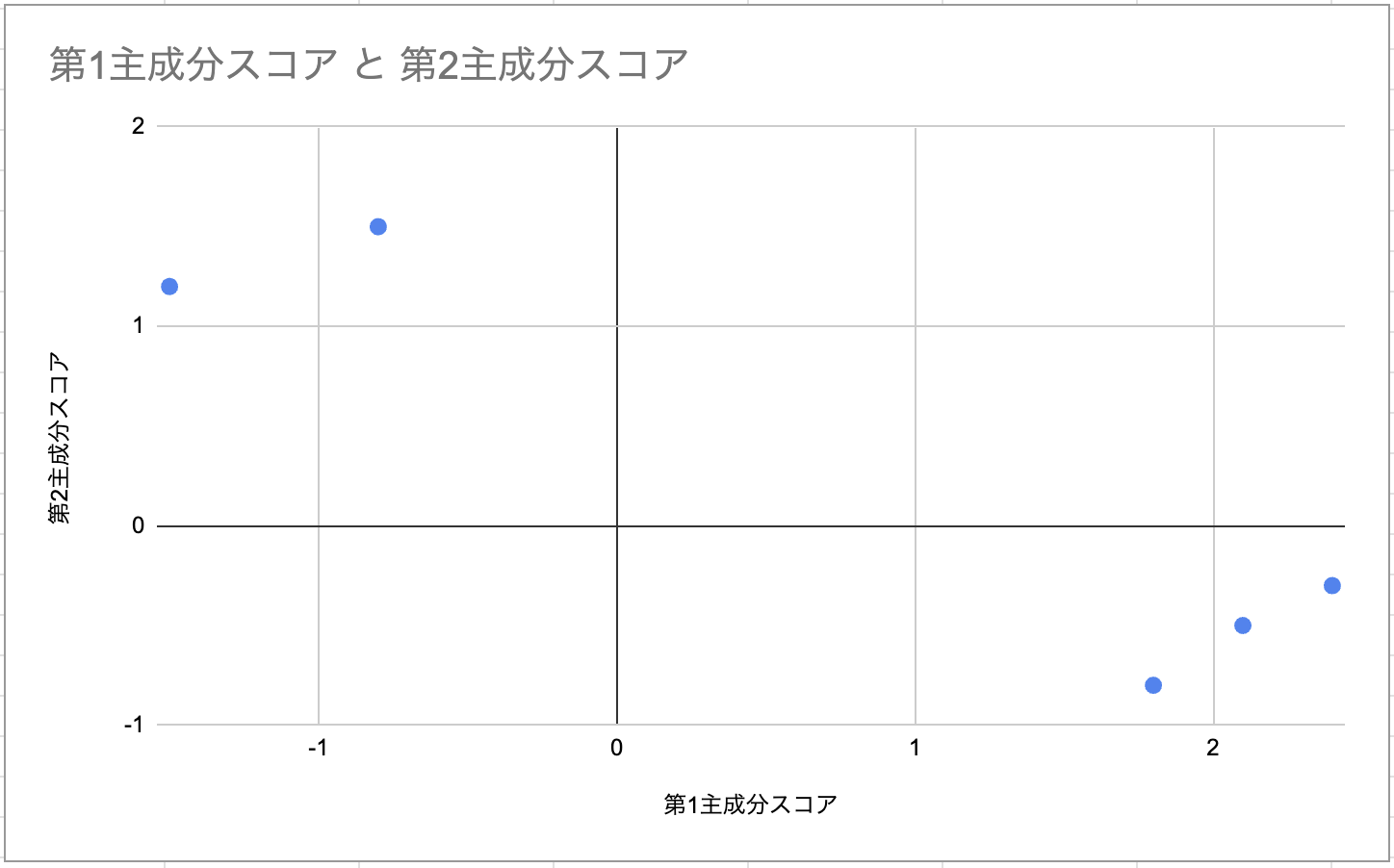
左上と右下によってますね。右下が第1主成分の影響が多く、左上が第2主成分の影響が大きい状況です。
皆さんもやってみよう!
こうして諸々の分析結果から・・・
7割の寄与率がある第1主成分の味・値段・ボリューム
2割の寄与率がある第2主成分の立地・居心地
としてより詳細にデータを解釈することができました。めでたしめでたし。
これでお店としては、なにを改善すべきかの優先度が見えてきたのではないでしょうか!
注意点ですが、主成分分析はあくまで影響度、つまり分散という観点での分析なので、この影響度の高い要素を改善すれば絶対にアンケート結果がよくなるということではありません。場合によっては今のがよかったのに、改善したせいで大きくマイナスになる可能性もある要素とも言えるかと思います。そこから先はデータサイエンティストではなく、経営者や料理人の範疇になりますが!
何はともあれ、こうして主成分分析という手法を活用することでデータをより深く解釈することができます。私のような優柔不断な人間でも適切な選択をする手助けをしてくれる頼れる武器ですね。Barで何を頼めばいいかわからないけどおろおろするのはかっこ悪いと思っている方は、自分のように同じものを頼み続けるか、主成分分析をしてみましょう。
ただし、次元を削減しすぎて選択肢が狭まっては豊かさがなくなってしまいます、人生には少しの迷いや余白が必要です。より良いと思われる最適な選択をし続けようとすることだけが本当に良い事なのかはわかりませんね。・・・とBarのマスターの受け売りでした。
皆さんの人生の主成分に乾杯!